21 Avril 2022
Transformation de Fourier
La transformation de Fourier est une opération inversible s’appliquant à certaines fonctions. C’est un outil important pour l’étude des fonctions et des signaux.
Intuition grâce aux polynômes
Commençons l’explication en partant de l’étude d’un cas plus simple et plus intuitif, qui nous servira par la suite pour comprendre ce que fait exactement cette transformée de Fourier.
Imaginons un polynôme quelconque d’ordre
Ce polynôme se décompose assez naturellement en une somme de monômes. Ces monômes forment une base des polynômes. Chaque polynôme peut ainsi être représenté par ses coordonnées dans cette base de monômes.
Ce résultat, bien que plutôt simple, est déjà extrêmement puissant. Si tous les polynômes peuvent être uniquement déterminés par leurs coefficients (i.e. leurs coordonnées dans la base canonique des monômes de plus petits degrés au sens large), alors nous pouvons inverser linéairement le problème et déterminer les coefficients d’un polynôme donné.
A partir d’un ensemble d’observations et résultats de mesure, nous pouvons alors trouver la meilleure approximation polynômiale du rapport entre observations et résultats. 1
Pour plus de simplicité, nous pouvons utiliser la notation suivante :
Pour résoudre ce système nous pouvons passer par les décompositions standards (LU, QR et SVD) et déterminer les solutions les plus satisfaisantes (e.g. au sens des moindres carrés ou limitant le bruit).
Sans aller dans les détails ici, pour ce genre d’approximations il peut être intéressant de choisir une autre base vectorielle pour l’ensemble des polynômes. Le problème de la base canonique est qu’elle n’est pas orthonormée : cela peut entraîner certaines complications dans le calcul numérique rendant les résultats inexploitables 2.
Pour cela nous pouvons par exemple remplacer la matrice introduite ci-dessus par la matrice composée des évalutations pour chaque observation des premiers polynômes de Legendre.
Tout ça pour aller où ?
Nous avons vu ici que déterminer une base vectorielle pour les polynômes d’un ordre donné quelconque nous permet de bien les étudier, les approximer, et les représenter d’une façon plus pratique notamment dans le calcul numérique.
A présent nous allons étendre ce processus à l’étude de fonctions réelles quelconques.
Commentaire pour le paragraphe « Intuition grâce aux polynômes »
Base des fonctions
Dans cette partie nous travaillons avec des fonctions de
Produit scalaire pour deux fonctions complexes
Pour avoir une notion d’orthogonalité, nous devons définir un produit scalaire dans l’espace préhilbertien des fonctions complexes :
Remarquons que :
Aussi, [à compléter]
Pour des raisons pratiques, nous privilégions davantage la base vectorielle formée d’exponentielles complexes.
Celle-ci existe simplement par le fait que :
Rappel de la formule d’Euler :
Nous avons maintenant une base orthogonale du plan complexe, prenons un vecteur de cette base :
Nous pouvons remarquer que c’est également un vecteur unitaire :
Nous avons donc bien une base orthonormée.
Séries de Fourier
Les séries de Fourier permettent d’exprimer des fonctions
Commentaire pour le paragraphe « Base des fonctions »
Définition de la transformée de Fourier
Comment étendre cela aux fonctions non périodiques ?
Pour cela, nous pouvons voir les fonctions non périodiques comme des fonctions périodiques mais de « période infinie ». La transformée de Fourier est alors définie pour toute fonction
La transformée de Fourier d’une fonction est unique et permet de la décrire totalement, à condition que celle-ci existe. C’est une autre représentation de la fonction.
Pour reprendre la terminologie utilisée dans la description des séries de Fourier, cette transformée est en quelque sorte une fonction des coordonnées de la fonction
Commentaire pour le paragraphe « Définition de la transformée de Fourier »
Fonction Dirac delta
Jusque-là l’idée de la transformée de Fourier peut se comprendre comme une extension par continuité des séries de Fourier. Cela généralise bien les choses puisqu’il nous est désormais possible d’exprimer une fonction dans l’espace vectoriel cité ci-dessus par une combinaison linéaire d’un ensemble de vecteurs non contable et continue.
Quid des combinaisons discrètes des vecteurs de bases ? Comment les exprimer ?
Pour cela nous introduisons une fonction un peu particulière : la fonction dirac delta.
La fonction dirac delta est une fonction réelle nulle pour tout réel non nul, et dont la valeur est indéterminée (cela dépend des conventions utilisées) en zéro. C’est un « pic ».
Remarquons maintenant assez naturellement que :
(Note : le facteur
Remarque importante : la fonction
Maintenant, si une fonction
Avec
Calculons maintenant sa transformée de Fourier :
Ressource sur la fonction dirac delta : chapter1 (ubc.ca)
Pour plus de remarques sur cette fonction particulière : Fonction delta de Dirac.
Commentaire pour le paragraphe « Fonction Dirac delta »
Inversion de la transformée
Naturellement, à partir de l’expression de la transformée de Fourier d’une fonction nous pouvons trouver la fonction originelle :
Commentaire pour le paragraphe « Inversion de la transformée »
Interprétation fréquentielle
Nous pouvons visualiser ça comme des fréquences
Très naturel dans l’étude du son
Compression des données
But what is the Fourier Transform? A visual introduction. - YouTube
Purrier Series (Meow) and Making Images Speak – Bilim Ne Güzel Lan (bilimneguzellan.net)
Commentaire pour le paragraphe « Interprétation fréquentielle »
Exemples pour mieux comprendre
Exemple 1
Soit un signal
Ce résultat est cohérent : le signal donné est issu d’une composition de deux exponentielles complexes, sa transformée est donc simplement composé de deux pics indiquant les paramètres des deux exponentielles complexes. Ces pics ont lieu lorsque
En effet, nous avons bien :
Exemple 2
Imaginons un signal comme celui-ci.
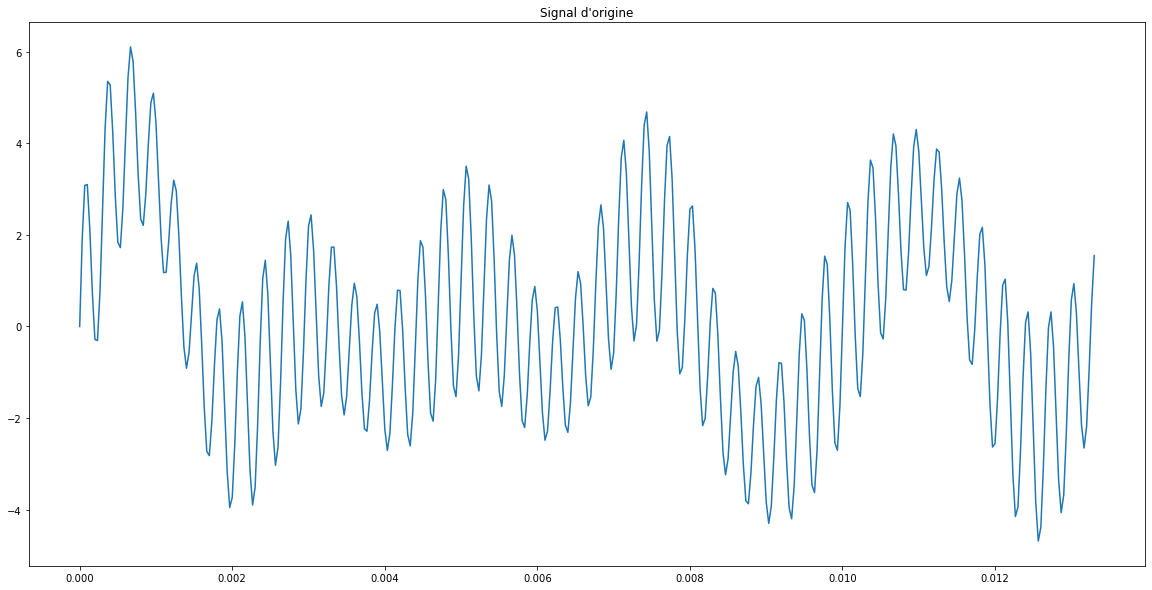
Cela pourrait représenter un enregistrement audio par exemple.
Prendre sa transformée de Fourier va nous permettre de déterminer les harmoniques de ce signal.
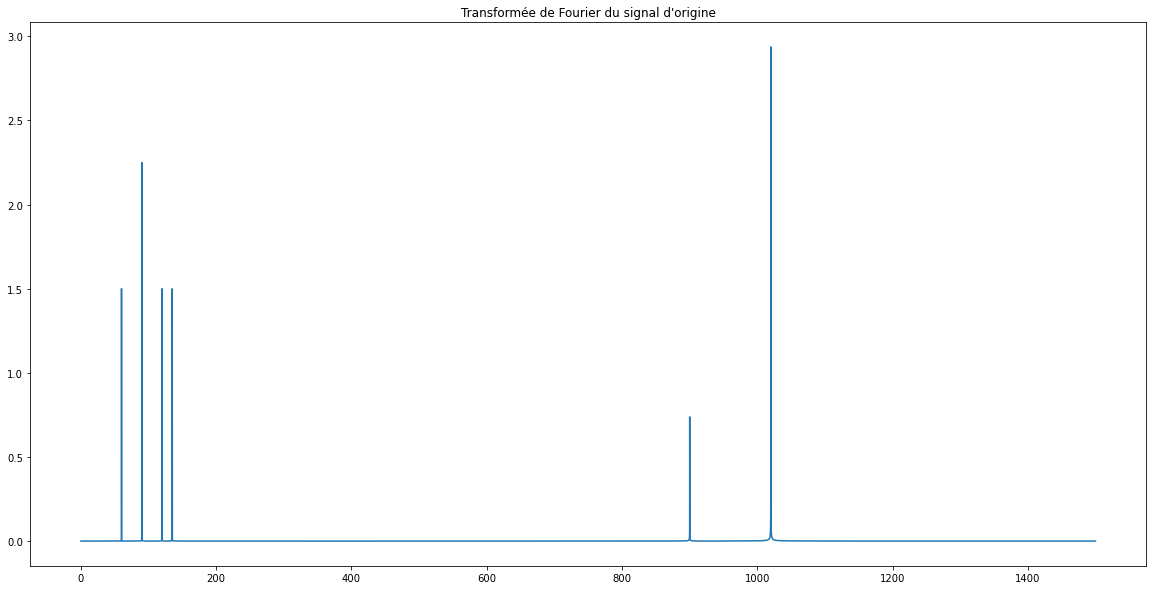
Dans un cas pratique, il pourrait être utile de supprimer les fréquences hautes ou basses.
Voici ce que cela donne pour ce signal :
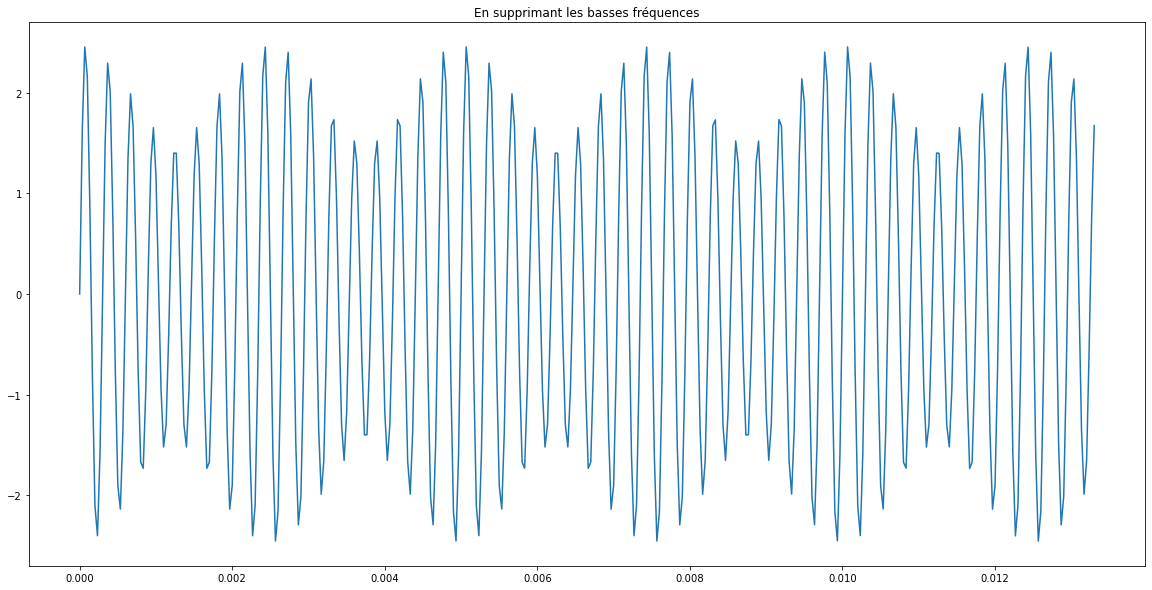
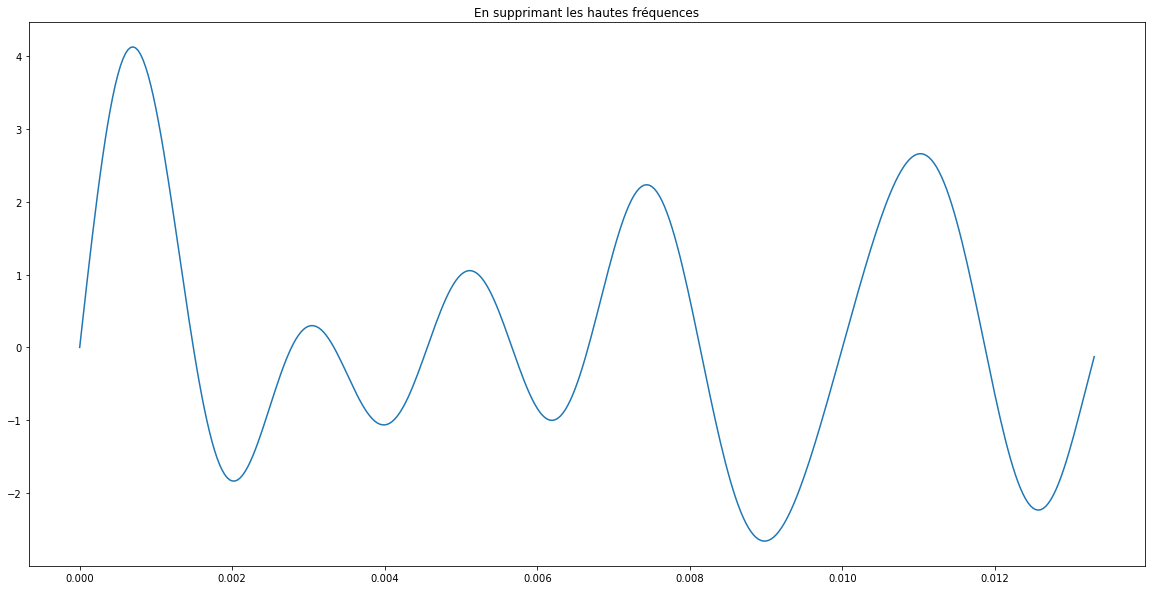
Commentaire pour le paragraphe « Exemples pour mieux comprendre »
Remarques
Nous avons traité ici uniquement des cas de fonctions / signaux continus. La transformée de Fourier existe également dans le cas de fonctions à pré-images discrètes / antécédents discrets.
La normalisation de la transformée de Fourier n'est pas systématique. Ainsi, en fonction du domaine d'application ou des conventions, on va préférer la définir avec ou sans normalisation. Le facteur
Les idées que l'on a évoqué ici peuvent également servir dans le domaine de la compression d'images :
Commentaire pour le paragraphe « Remarques »
- Matrice de Vandermonde — Wikipédia↩
- Un mauvais conditionnement peut mener à des résultats inexploitables. La discrétisation des valeurs utilisées tout au long du calcul en est la principale cause.↩
- Espace Lp — Wikipédia↩
Les suggestions sont activées pour cette page. N'hésitez pas à faire des remarques sur les différents paragraphes.